Refereed paper by Kadri, F.L. and Duncan, I.J.,
published in Behavioural Processes v.33 (1995) pp. 273-288
To propose a mathematically rigorous dynamic nonlinear model of motivation combining priming and homeostatic mechanisms.
Minimum recommended background:
1- Working knowledge of Laplace Transforms
2- Basic knowledge of Multidimensional Laplace Transform (MLT) techniques, see for example chapters 1 to 7 in book: Schetzen, M, "The Volterra and Wiener Theories of Nonlinear Systems", Wiley, New York 1980.
There is considerable agreement among academics over the definitions of two types of animal motivations: Priming, which increases the likelihood of a stronger response with the repetition of appropriate stimuli, and homeostasis as the regulating mechanism which corrects deviation from a preferred level of a body chemical or physical variable. Animal behavior often shows aspects of both motivations, therefore a realistic model of behavior should have representation of both motivational mechanisms.
Simulation of priming is straight forward; the repeating of priming stimulus is initially cumulative, then saturation sets in after frequent repetition, this is represented by a slow dynamic system followed by a nonlinear element described by a positive output y value for input x near zero for an unprimed state, then rising until saturation in the vicinity of x=1 representing a primed state. The primed response is represented simply by the product of the priming stimulus with a constant strength behavior represented by a pulse of short duration.
The definition of homeostasis masks the difference between behavioral and physiological regulation. Maintaining physiological balances such as temperature, blood sugar level and enzymes are performed involuntarily and can be modeled by linear negative feedback loops, while behavioral regulation is governed by triggered patterns of behavior which occur in episodes, and the response is obviously nonlinear since stimuli applied at the sated state do not invoke any response. Here, a new representation of behavioral homeostasis is used where the stimuli are the pulses received from the priming mechanism and the regulating element is a multiplier. The feedback path to the multiplier is modulated by a nonlinear element with positive output y value near zero input x representing a state of hunger, and approaching a zero y value in the vicinity of x=1 representing a state of satiation. The mechanism works when receiving a stimulus in hungry x=0 mode the stimulus is modulated by the positive value of y, and when sated then the multiplicand value of y is near zero and the stimulus is severely attenuated.
The combination of priming and homeostasis in tandem is represented by the dynamic block diagram below. The choice of parameter values is arbitrary, selected in order to model the states of unprimed/primed at 0 and 1v input to the priming element and the states of hungry/sated at 0 and 1v at the multiplier feedback element.
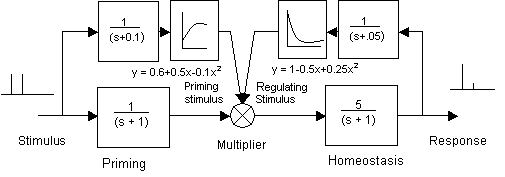
Fig. A1 Block diagram of dynamic nonlinear simulation of a priming-homeostatic motivational process.
The four motivational classes are represented by the dynamic system above; self-preservation or emotional motivation is represented by only priming while feeding, sociosexual and parenting motivations contain both priming and homeostatic mechanisms.
The MLT representation of the above characterizes the system completely. In the simulation run the system was subjected to trains of impulses which in combination together lead to tracing the characteristic nonlinear kernels. The kernels in effect describe the behavior of the system and its response to any arbitrary stimulus. Notice that the system accepts trains of impulses as stimuli and therefore could simulates realistically neuronal networks which in reality respond to brain impulse signals.





